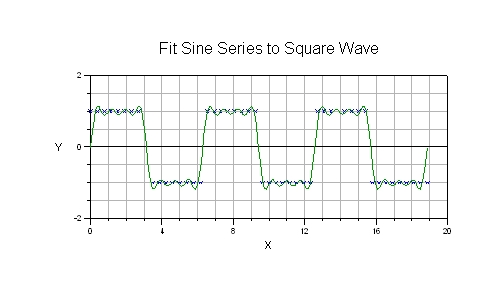
This example fits a function involving a sine series to a square wave.

Fourier showed that the sum of a series of sine functions with odd coefficients of the angle could model a square wave if the appropriate multipliers were chosen for each of the sine terms. A perfect fit would require an infinite number of sine terms. In this example, we fit a sine series with four terms to a square wave.

Here are the NLREG statements to fit this function:

Title "Fit Sine Series to Square Wave";
Variables X,Y;
Parameters p0,p1,p3,p5,p7;
Function y = p0 + p1*sin(x) + p3*sin(3*x) + p5*sin(5*x) + p7*sin(7*x);
Plot;
Data;
[ data goes here ]

Here is a plot generated by NLREG showing the function fitted to a a square wave set of values.